Monty Hall Problem
- Nandu Sreevalsan

- Mar 16, 2019
- 1 min read
Updated: Jul 13, 2019
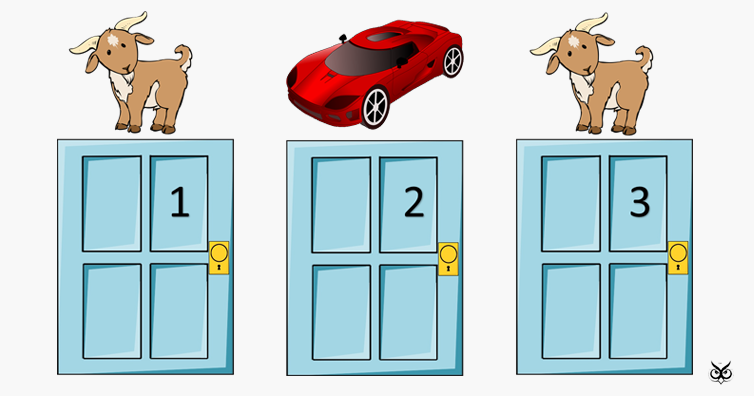
Monty hall problem (Wikipedia):
"Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?"
When I heard this problem for the first time, I thought it won't matter if you switch the choice, probability will be 50 - 50. Since you got only two choices, right, after one got eliminated. But the actual answer is you tend to increase your probability of winning to 66.7% if you switch.
Counter intuitive isn't it.
I tried this game with four different people, a total of 600 games and got a winning probability of around 65% if you switch the option and 35% if you keep the same choice. Tried the same with software simulation using python random module and got similar results.
The best way to explain the solution is as following:
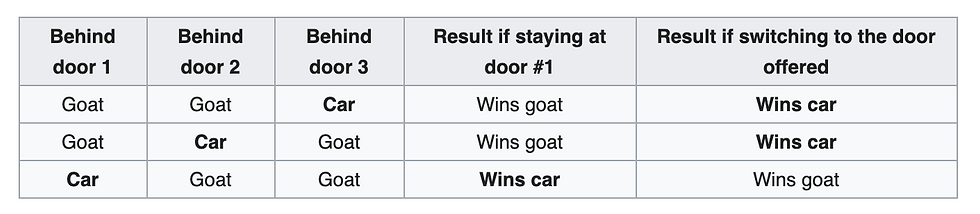
There are only three outcomes , one, you select the car, second, you select a goat, third, you select a goat.
So, If your selection was the car at first, you will lose if you switch, but if you have selected the goat, you will win the car if you switch. So, the winning probability if you switch is 2/3, refer Fig 1.
Still not convinced, try playing the game with your friends and see the results for yourselves.


Comments